Remediation TimeFrame Estimate Using Segmented Regression

Segmented regression is a powerful statistical tool for improving remediation timeframe estimates by accounting for changes in contaminant concentration trends over time. Unlike traditional single-slope regression methods, segmented regression identifies breakpoints in monitoring data and applies distinct linear trends to different phases of plume behavior, such as rapid initial decline and long-term tailing. This approach better reflects evolving site conditions, remedy performance, and attenuation dynamics, which produces more realistic and defensible projections of cleanup timelines.

Statistical Basis for Demonstrating the Absence of Soil Contamination

This post summarizes statistically defensible methods used to demonstrate, with specified confidence, the absence of soil contamination relative to regulatory action levels. It presents exceedance-based, mean-based, percentile-based, and hotspot-detection frameworks, emphasizing how sampling design, confidence, power, and variability, rather than site area alone, govern sample size and decision reliability.

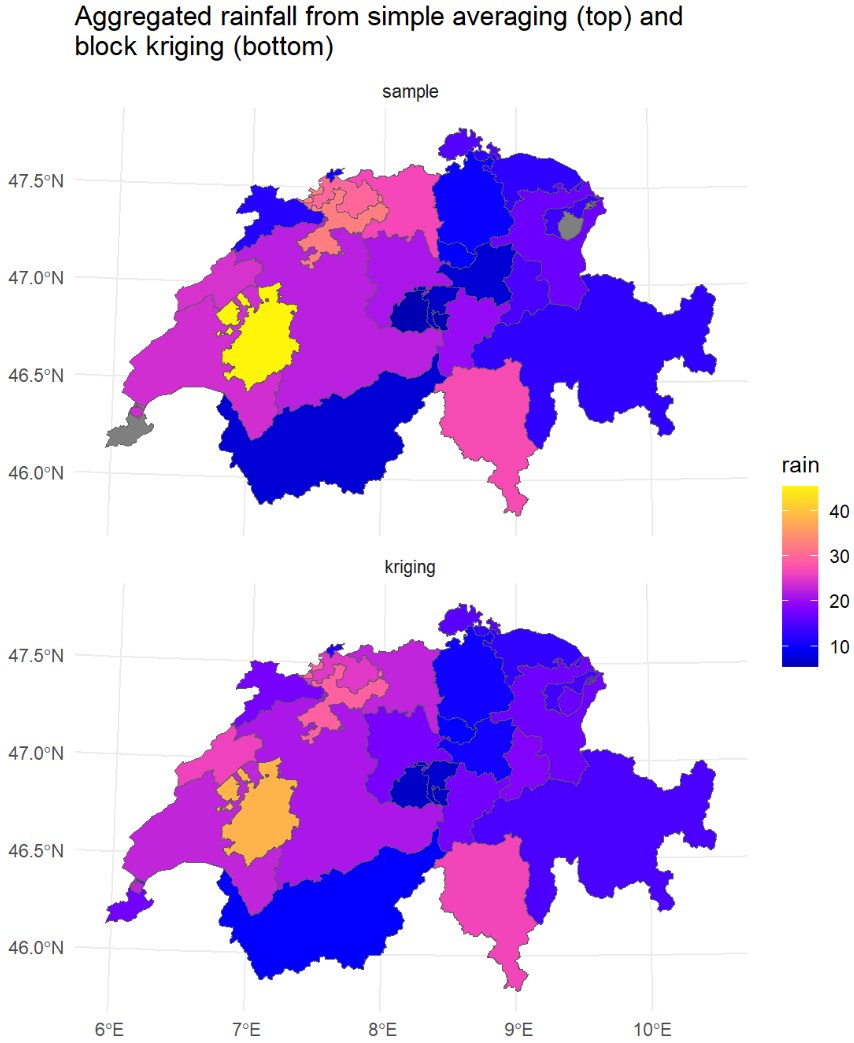
Block Kriging

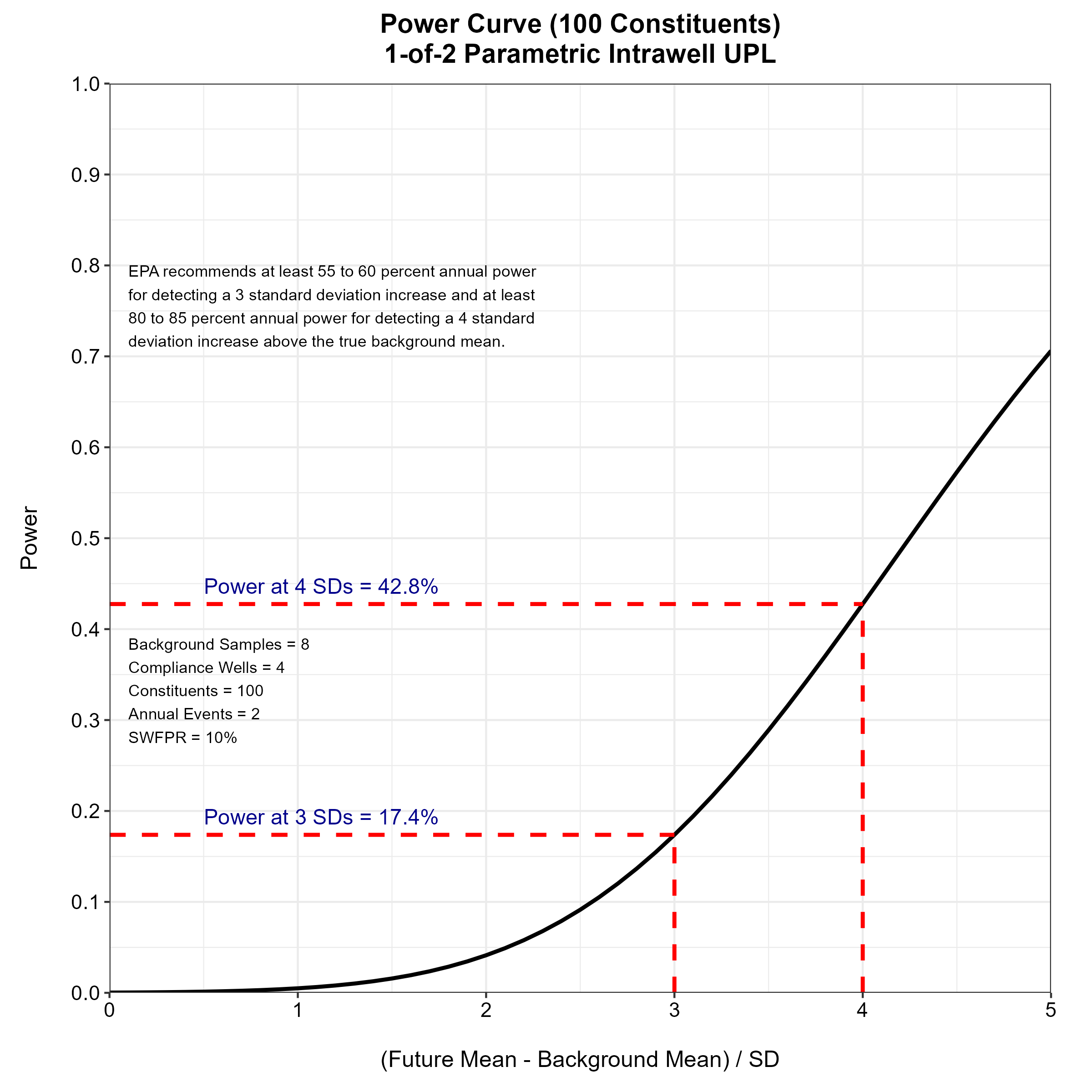
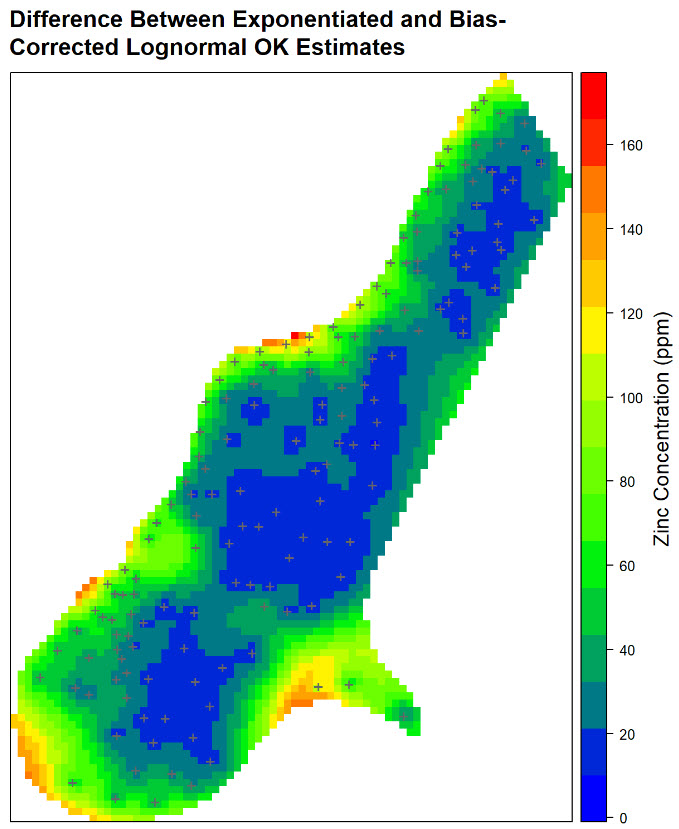
This post explores block kriging as a geostatistical method for estimating average values over defined areas, contrasting it with point kriging. Using daily rainfall measurements in Switzerland and the R gstat package, the analysis demonstrates how block kriging produces smoother maps and lower estimation variance compared to point kriging. While acknowledging the potential for obscuring true data variability, the post highlights block kriging’s utility when focusing on values over larger spatial supports, yielding less variable and more accurate areal mean predictions than simple averaging.

Groundwater Detection Monitoring: Importance of Limiting the Number of Constituents

Detection monitoring uses statistical analyses to differentiate natural groundwater variations from those due to landfill activities. These monitoring programs prioritize two key performance characteristics: adequate statistical power and a low sitewide false positive rate (SWFPR), distributed across all annual statistical tests. Fewer tests result in a lower single-test false negative error rate, and therefore an improvement in statistical power. To illustrate this concept, the per-test false positive rate and the corresponding power for semiannual testing at four compliance wells will be calculated, first considering 10 constituents and then 100 constituents. This post aims to correct the misconception that increasing the number of constituents enhances the statistical power of detection monitoring.

Test for Stochastic Dominance Using the Wilcoxon Rank Sum Test

The two-sample Wilcoxon Rank Sum (WRS) is often perceived as a median comparison procedure based on the assumption that two populations differ only by a consistent shift, a condition that is infrequently met in practice. Its actual purpose is to determine if one distribution stochastically dominates another. This post seeks to clarify the WRS test’s true function through a simulation involving two samples with the same medians but different distributions. In cases of non-symmetric data, alternative methods such as quantile regression and bootstrapping are recommended, offering nonparametric alternatives that do not rely on rank-based assumptions.

Statistical Properties of Autocorrelated Data

In classical statistical analysis, positive autocorrelation leads to an underestimation of the standard error because standard methods assume independence of data. This underestimation results in inflated test statistics, increasing the risk of incorrectly rejecting the null hypothesis. Autocorrelated data implies that each observation is related to nearby values, reducing the degrees of freedom and making the effective sample size smaller than the actual sample size. Monte Carlo simulation is used to explore the effect of autocorrelation on a hypothesis test to determine whether an observed data set is drawn from a population with mean zero.

Lognormal Kriging and Bias-Corrected Back-Transformation

Kriging assumes spatial stationarity and does not require a specific distribution for estimated variables. However, non-symmetric distributions, often found in earth sciences, can complicate variogram calculations and lead to over-prediction, especially when high values are present. To address these challenges, data are often transformed using the natural logarithm. A challenge occurs during back-transformation of predictions and variances from the log scale to the original scale, as simple exponentiation is insufficient due to the weighted sums in log-transformed data. This post will explore the mathematical formulations essential for effective back-transformation in lognormal kriging.

Predictive Modelling of Traffic Accidents in the U.S.

Motor vehicle accidents are an important part of traffic safety research. Analyzing the factors contributing to accidents and accident severity is critical for enhancing road safety standards. In this post, traffic accident data patterns will be explored and studied using machine-learning analysis techniques.

Generalized Least Squares Regression

In OLS regression, assumptions such as independent and identically distributed errors are important for accurate estimation and inference. Heteroskedasticity, or unequal variances of residuals, can lead to biased estimates and incorrect standard errors. Alternatives to OLS, such as GLS and WLS regression, can be considered when OLS assumptions are violated. GLS is used for dependent errors, while WLS is used for independent but non-identically distributed errors.

Weighted Least Squares Regression

Heteroscedasticity in regression analysis refers to varying levels of scatter in the residuals. Its presence affects OLS estimators and standard errors, leading to biased estimates and misleading results. When errors are independent, but not identically distributed, weighted least squares regression can be used to address heteroscedasticity by placing more weight on observations with smaller error variance. This results in smaller standard errors and more precise estimators.