Introduction

A fundamental assumption of many statistical tests is that sample data are independent and identically distributed, meaning that observations over time should lack clear time dependence or significant autocorrelation. Time dependence involves the presence of trends or cyclical patterns in a time series plot, while autocorrelation measures how much future values can be predicted from past measurements. Strong autocorrelation indicates predictability between consecutive values, whereas independent values vary in a random, unpredictable manner.

Many types of time series exhibit significant autocorrelation. Autocorrelation in time series data can significantly distort statistical test results by artificially reducing p-values, leading to an increased risk of Type I errors (false positives). This issue affects standard hypothesis tests, such as ANOVA, t-tests, chi-squared tests, and trend analysis, which rely on the assumption of independence of observations. Autocorrelation increases the variance of sample means, inflating test statistics and causing erroneous rejection of null hypotheses. Consequently, applying these tests to environmental data without addressing autocorrelation can yield misleading conclusions.

In this blog post, time series will be used to illustrate the effects of positive autocorrelation on the outcome of hypothesis tests. Monte Carlo simulation will be used to explore the effect of temporal autocorrelation on the outcome of a hypothesis test that an observed data set is drawn from a population with mean zero.

Hypothesis

Suppose we have measured a set of values \({\{Y_1,Y_2,\dots,Y_n\}}\) of a normally distributed random variable Y whose mean \(\mu\) and variance \(\sigma^2\) are unknown:

$$Y_i = \mu + \varepsilon_i, \quad i = 1,\dots,n$$

where the \(\varepsilon_i\) are independent, identically distributed random variables drawn from a normal distribution with mean zero and variance \(\sigma^2\). The sample mean \(\hat{Y}\) is given by:

$$\hat{Y} = \frac{1}{n}\sum_{i = 1}^{n} Y_i$$

If the \(Y_i\) are independent, the variance of \(\hat{Y}\) is given by:

$$var\{\overline{Y}\} = \frac{\sigma^2}{n}$$

and the sample variance is defined by:

$$s^2 = \frac{1}{n - 1}\sum_{i = 1}^{n} (Y_i - \overline{Y})^2$$

which is an unbiased estimator of \(\sigma^2\). Therefore \(\sigma^2/n\) is an unbiased estimator of the variance of \(\overline{Y}\). The square root of this quantity is called the standard error and is given by:

$$s\{\overline{Y}\} = \frac{\sigma^2}{\sqrt{n}}$$

We wish to test the null hypothesis that the value of the mean \(\mu\) is zero against the alternative that it is not:

$$ \begin{split} H_0: \mu = 0 \\ H_a: \mu \ne 0 \end{split} $$

When the population from which the values \(Y_i\) are drawn is normal, this hypothesis can be tested using the Student t statistic given by:

$$t = \frac{\overline{Y} - \mu}{s\{\overline{Y}\}}$$

Temporal Autocorrelation

Autocorrelation takes the form of a first-order autoregressive time series in the error terms given by (Kendall and Ord 1990):

$$ Y_i = \mu + \eta_i \ \eta_i = \lambda\eta_i + \varepsilon_i, \quad i = 1, 2, \dots $$

where \(-1<\lambda<1\) and the \(\varepsilon_i\) are independent, identically distributed random variables drawn from a normal distribution with mean zero and variance \(\sigma^2\). The \(\eta_i\) are the autoregressive error terms. This can be simplified by substituting:

$$ \begin{split} \eta_i = Y_i - \mu \\ \eta_{i-1} = Y_{i-1} - \mu \end{split} $$

into the above equation to get the following:

$$Y_i - \mu = \lambda(Y_{i-1} - \mu) + \varepsilon_i, \quad i = 1, 2, \dots$$

For the null hypothesis, \(\mu\) is set to zero and the equation becomes:

$$Y_i = \lambda Y_{i-1} + \varepsilon_i, \quad i = 1, 2, \dots$$

Let’s run 10,000 simulations to explore the effect of temporal autocorrelation on the outcome of a t-test with autocorrelated data for \(\lambda\) ranging from 0 to 0.9. Each simulation will use a sample of size 10. The initial value is set at \(Y_1 = 0\), which is a fixed, non-random number. This may cause the data to be non-stationary for the first few values of i. To avoid this, twenty values of \(Y_i\) will be generated and the last ten values will be used for each simulation.

# Set initial values 
error.rate <- numeric(10)
mean.Y <- numeric(10)
sd.Y <- numeric(10)
sem.Y <- numeric(10)
lambda <- seq(0.0, 0.9, 0.1)

# t-test function
ttest <- function(lambda) {
  Y <- numeric(20)
  for (i in 2:20) Y[i] <- lambda * Y[i - 1] + rnorm(1, sd = 1)
  Y <- Y[11:20]
  t.ttest <- t.test(Y, alternative = 'two.sided')
  TypeI <- as.numeric(t.ttest$p.value < 0.05)
  Ybar <- mean(Y)
  Yse <- sqrt(var(Y) / 10)
  return(c(TypeI, Ybar, Yse))
}

# Monte Carlo simulation
set.seed(123)
for (j in 1:10) {
  set.seed(1)
  U <- replicate(10000, ttest(lambda[j]))
  error.rate[j] <- mean(U[1,])
  mean.Y[j] <- mean(U[2,])
  sem.Y[j] <- mean(U[3,])
  sd.Y[j] <- sd(U[2,])
}

Now that we have ran the simulations, let’s plot the results.

par(mfrow = c(2, 2), mai = c(0.8, 0.8, 0.3, 0.2))
# Plot error rate
plot(
  lambda, error.rate,
  pch = 16, cex = 1.2, cex.lab = 1.2,
  xlab = expression(lambda),
  ylab = 'Error Rate'
)
title(main = 'Error Rate', cex.main = 1.1)

# Plot mean of sample means
plot(
  lambda, mean.Y,
  pch = 16, cex = 1.2, cex.lab = 1.2,
  ylim = c(-0.1, 0.1),
  xlab = expression(lambda),
  ylab = expression(Mean~italic(bar(Y)))
)
title(main = 'Mean of Sample Means', cex.main = 1.1)

# Plot mean estimated standard error
plot(
  lambda, sem.Y,
  pch = 16, cex = 1.2, cex.lab = 1.2,
  ylim = c(0, 0.5),
  xlab = expression(lambda),
  ylab = expression(Mean~"s{"*italic(bar(Y))*"}")
)
title(main = 'Mean Estimated Standard Error', cex.main = 1.1)

# Plot standard deviation of mean
plot(
  lambda, sd.Y,
  pch = 16, cex = 1.2, cex.lab = 1.2,
  ylim = c(0, 2),
  xlab = expression(lambda),
  ylab = expression("Std. Dev. of "*italic(bar(Y)))
)
title(main = 'Standard Deviation of Mean', cex.main = 1.1)

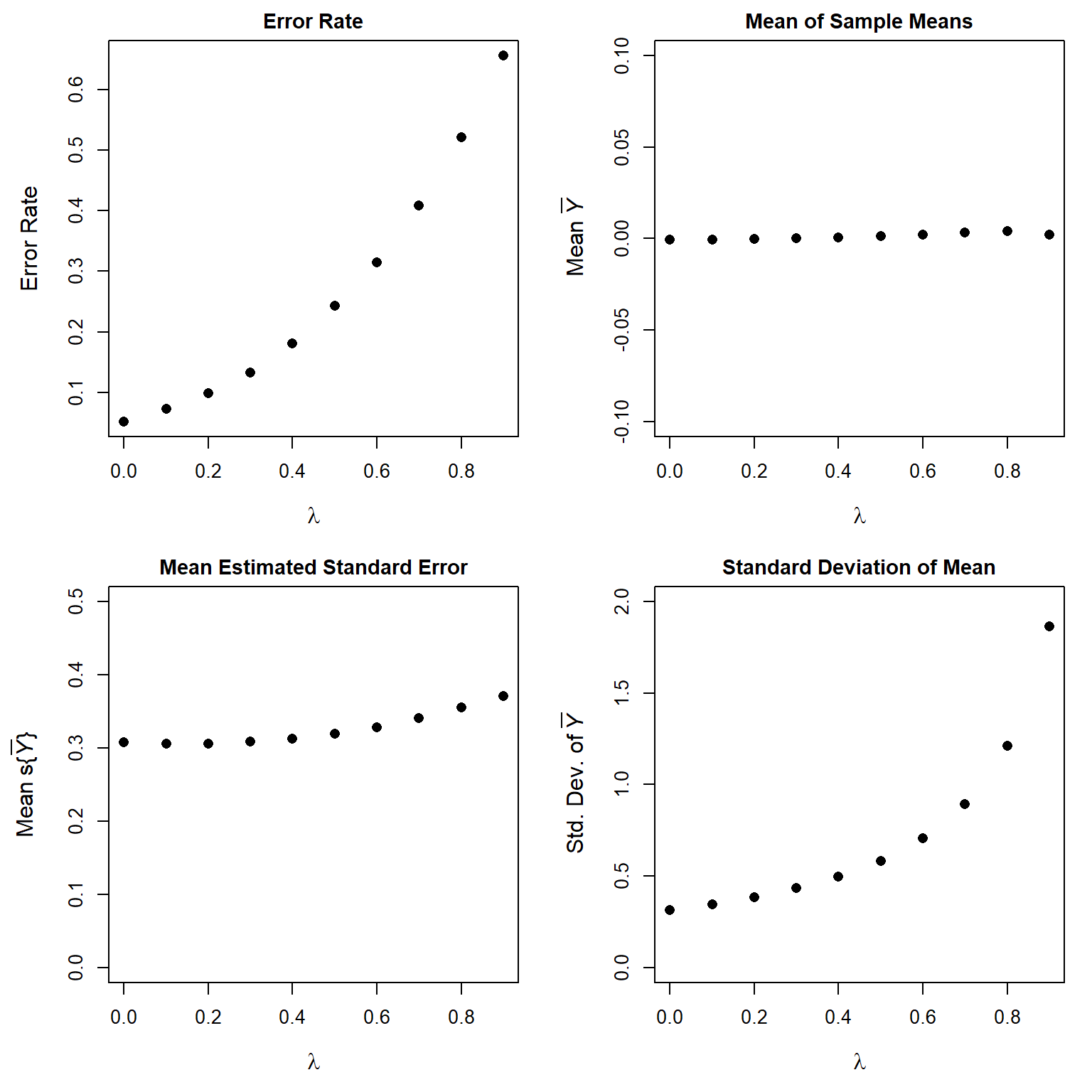
The Type I error rate increases dramatically with increasing \(\lambda\). Meaning, that a positive autocorrelation increases the likelihood of rejecting the null hypothesis when it might be true (the probability of the Type I error becomes larger than what the attained significance level indicates). This occurs because the actual standard deviation of \(\overline{Y}\) increases dramatically as \(\lambda\) increases from zero. In the presence of temporal autocorrelation, \(s\{\overline{Y}\} = s/\sqrt{n}\) underestimates the true standard deviation of \(\overline{Y}\), resulting in a smaller denominator for the t statistic than it should be. This causes the t statistic to be inflated, consequently increasing the Type I error rate.

Spatial Autocorrelation

The results presented above suggest that positive autocorrelation in time series random variables increases variance. This concept applies similarly to spatially autocorrelated random variables. Classical sampling methods usually rely on the assumption that each population member has a equal probability of selection. However, in practice, unrestricted random sampling of spatially autocorrelated data is not always conducted. Instead, a grid-based approach is utilized to select a subset of the population. Although this approach is implemented to enhance parameter estimates, the presence of spatial autocorrelation can lead to unreliable mean and standard error estimates. The inherent correlation among nearby samples is often overlooked in design-based inference, even though it’s considered in model-based inference.

Spatial autocorrelation presents both advantages and challenges in spatial analysis. It can be advantageous when it provides useful insights for understanding processes based on observed patterns. However, in many cases, spatial autocorrelation is seen as a major drawback for hypothesis testing and prediction since it violates the assumption of independently and identically distributed errors that most traditional statistical methods rely on, thereby increasing the risk of Type I errors. As the spatial autocorrelation inherent in georeferenced data increases, so does the redundancy of information within that data.

Conclusion

In classical statistical analysis, positive autocorrelation can result in an underestimation of the standard error. This occurs because standard statistical methods generally assume that the data are independent and identically distributed. When standard errors are underestimated, test statistics become artificially high, increasing the likelihood of incorrectly rejecting the null hypothesis when it is actually true. In cases of autocorrelated data, each data point contains information about neighboring values, which decreases the degrees of freedom compared to independent data. Consequently, the effective sample size is smaller than the actual sample size.

References

Kendall, M. and J.K. Ord. 1990. Time Series. Edward Arnold, Kent, Great Britain.