Nonparametric Two-Way ANOVA
By Charles Holbert
April 16, 2022
Introduction
Often data from more than two groups within a single factor needs to be evaluated, usually on the basis of a representative value from each group. For uncensored data, comparisons among groups are made using the parametric analysis of variance (ANOVA) and the nonparametric Kruskal-Wallis (KW) test. These tests determine whether the groups essentially belong to the same underlying population, or whether there are significant differences between the group distributions. This is the simplest type of ANOVA design and is called one-way ANOVA. Two-way ANOVA is when two factors or variables potentially affect the response variable. For conventional two-way ANOVA with several observations or data values for each combination of factors, it is possible to test for factor interaction. Factor interaction refers to the case where each factor not only exerts an effect on the response variable (described as main effects), but also may interact with the other factor or factors to exert additional joint effects on the response variable (known as interaction effects)
If the data meet normality and homoscedasticity (i.e., equality of variance) requirements of parametric ANOVA, methods are available for computing two-way ANOVA. However, the KW test for nonparametric ANOVA cannot be directly extended to the case where there are two or more factors as is done with parametric two-way ANOVA. Instead, a nonparametric approximate approach is to transform the data values. One method that is not unduly affected by violations of the normality and homoscedasticity assumptions of parametric ANOVA is to transform the data values to their ranks, and then compute a parametric two-way ANOVA on the data ranks. This rank transformation procedure can be used to determine whether the ranks differ from group to group. Post-hoc comparisons can be performed on the data ranks to determine which groups are different from each other. An alternative approach is to use ordinal logistic regression to provide general contrasts on the log odds ratio scale (Harrell 2015).
In this post, we will evaluate whether sample depth and/or site location affect arsenic concentrations measured in soil. To address non-normality and heteroscedasticity, two-way ANOVA will be performed using the rank-transformation of the data values.
Data
Arsenic concentrations were measured in soil from two depth intervals, shallow (SS) and deep (SB), at five sites (RA1 through RA5). We would like to determine whether arsenic concentrations in soil not only exhibit spatial variability between site locations but also may be affected by sample depth. This constitutes a two-way ANOVA problem, with one factor as location (represented by the five sites) and the second factor as matrix (represented by the two soil sample depths).
First, let’s load the data from the comma-delimited file and then make the LOCATION and MATRIX variables ordered factors.
# Load libraries
library(dplyr)
library(car)
# Load data
dat <- read.csv('data/Soil_Arsenic.csv', header = T)
dat$LOGDATE <- as.POSIXct(dat$LOGDATE, format = '%m/%d/%Y')
# Make matrix variable ordered factor
dat$MATRIX <- factor(
dat$MATRIX, ordered = TRUE,
levels = c('SS', 'SB')
)
# Make matrix variable ordered factor
dat$LOCATION <- factor(
dat$LOCATION, ordered = TRUE,
levels = c('RA1', 'RA2', 'RA3', 'RA4', 'RA5')
)
str(dat)
## 'data.frame': 266 obs. of 11 variables:
## $ LOCATION: Ord.factor w/ 5 levels "RA1"<"RA2"<"RA3"<..: 3 3 3 3 3 3 3 3 3 3 ...
## $ SACODE : chr "N" "N" "N" "N" ...
## $ LOGDATE : POSIXct, format: "2019-08-15" "2019-08-15" ...
## $ MATRIX : Ord.factor w/ 2 levels "SS"<"SB": 1 1 1 1 1 1 1 1 1 1 ...
## $ MEDIA : chr "Soil" "Soil" "Soil" "Soil" ...
## $ DILUTION: int 1 1 1 1 1 1 1 1 1 1 ...
## $ PARAM : chr "Arsenic" "Arsenic" "Arsenic" "Arsenic" ...
## $ DETECTED: chr "Y" "Y" "Y" "Y" ...
## $ RESULT : num 2.95 2.83 2.96 2.55 4.02 3.7 3.52 3.03 3.27 3.52 ...
## $ MDL : num 1 0.8 0.8 0.8 0.8 1 0.8 0.8 0.8 0.8 ...
## $ UNITS : chr "ppb" "ppb" "ppb" "ppb" ...
We see that the data contain 266 observations and 11 variables. Let’s create a frequency table to see how the observations are distributed between the MATRIX and LOCATION groups.
# Create frequency table
with(dat, table(LOCATION, MATRIX))
## MATRIX
## LOCATION SS SB
## RA1 25 23
## RA2 25 11
## RA3 25 25
## RA4 25 7
## RA5 25 75
For the SS soil depth, there are 25 samples per location. For the SB soil depth, the sample size ranges from 7 for RA4 to 75 for RA5. Thus, we have an unbalanced design. When sample sizes are substantially dissimilar, accurate interpretation of the main and interaction effects of the factors on the response variable becomes complicated, and the unequal sample sizes have a confounding effect on the factors.
Let’s calculate summary statistics for each data group.
# Compute summary statistics
dat %>%
group_by(MATRIX, LOCATION) %>%
summarise(
count = n(),
mean = round(mean(RESULT, na.rm = TRUE), 2),
median = round(median(RESULT, na.rm = TRUE), 2),
sd = round(sd(RESULT, na.rm = TRUE), 2),
cv = round(sd/mean, 2),
) %>%
ungroup()
## # A tibble: 10 x 7
## MATRIX LOCATION count mean median sd cv
## <ord> <ord> <int> <dbl> <dbl> <dbl> <dbl>
## 1 SS RA1 25 6.37 6.12 1.57 0.25
## 2 SS RA2 25 8.54 8.48 1.46 0.17
## 3 SS RA3 25 3.59 3.27 1.01 0.28
## 4 SS RA4 25 7.21 7.17 2.04 0.28
## 5 SS RA5 25 6.6 6.68 0.8 0.12
## 6 SB RA1 23 4.82 3.62 3.01 0.62
## 7 SB RA2 11 4.58 4.57 2.83 0.62
## 8 SB RA3 25 3.1 3.09 0.61 0.2
## 9 SB RA4 7 4.57 4.2 3.04 0.67
## 10 SB RA5 75 6.33 6.24 0.64 0.1
As expected, the central tendency and spread in arsenic concentrations vary between sample depth and location. The highest variability in concentration is associated with samples collected from the SB soil depth at locations RA1, RA2, and RA4.
Let’s visually inspect the data using box plots and an interaction plot. Box plots show the central tendency, degree of symmetry, range of variation, and potential outliers of a data set. The upper value of the box represents the 75th percentile for the data and the lower value of the box is the 25th percentile for the data. Thus, 50 percent of the data fall within the box. The top of the whisker represents the 75th percentile plus 1.5 times the interquartile range (IQR), where the IQR is the 75th percentile minus the 25th percentile. The bottom of the whisker is the 25th percentile minus 1.5 times the IQR. Any value outside of this range is considered a potential statistical outlier, which is represented by a dot on the plot. An interaction plot displays the levels of one variable on the x-axis and has a separate line for the means of each level of the other variable. The y-axis is the dependent or response variable. We will use the R package ggpubr to create the plots.
# Load library
library(ggpubr)
library(cowplot)
# Box plot
p1 <- ggboxplot(
dat, x = 'LOCATION', y = 'RESULT', fill = 'MATRIX',
palette = c('#257ABA', '#C9B826')
)
# Line plot
p2 <- ggline(
dat, x = 'LOCATION', y = 'RESULT', color = 'MATRIX',
add = c('mean_se', 'dotplot'), size = 1,
palette = c('#257ABA', '#C9B826'))
plot_grid(p1, p2, ncol = 1, align = 'v')
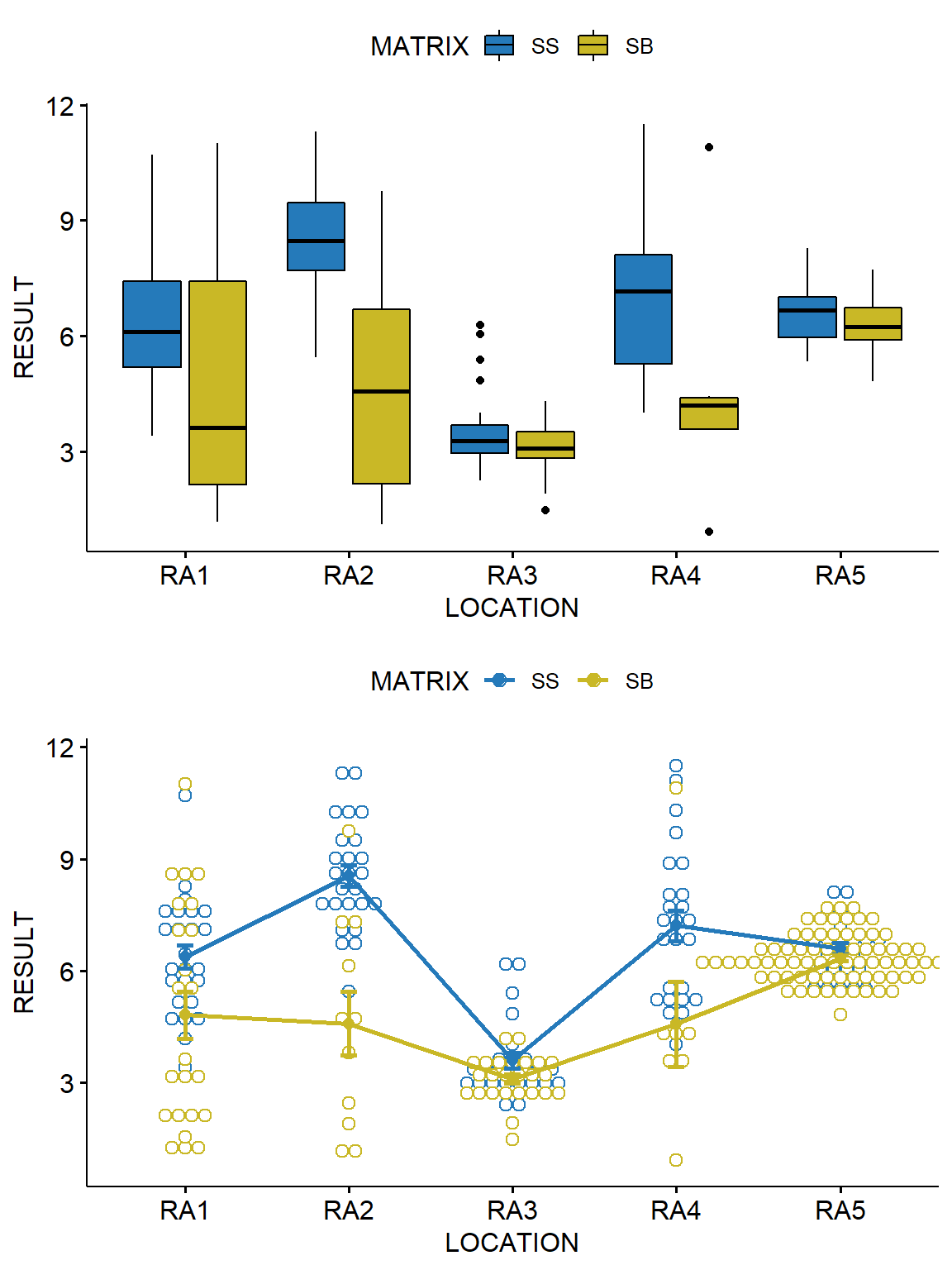
Based on these plots, it appears that arsenic concentrations are significantly different across the two soil depths for locations RA2 and RA4.
Two-Way ANOVA
Two-way ANOVA with replication can be used to test three null hypotheses: that the means of observations grouped by one factor are the same; that the means of observations grouped by the other factor are the same; and that there is no interaction between the two factors. When the interaction term is significant, each factor is evaluated separately using a one-way ANOVA.
Unbalanced two-way ANOVA is generally performed using Type-III sum of squares (SS). Estimates based on Type-III SS tell us how much of the residual variability in the response variable Y can be accounted for by factor A after having taken into account factor B and the A:B interaction, and how much of the residual variability in Y can be accounted for by factor B after having taken into account factor A and the A:B interaction. When using Type-III SS, factors should be set to use effects coding rather than relying on the default treatment codes. This can be done by adding the appropriate sum to zero contrasts as an argument to R’s aov function.
Let’s first perform two-way ANOVA on the original data.
# ANOVA procedure on original data
aov.org <- aov(
RESULT ~ MATRIX * LOCATION, data = dat,
contrasts = list(
MATRIX = 'contr.sum',
LOCATION = 'contr.sum'
)
)
Anova(aov.org, type = 'III')
## Anova Table (Type III tests)
##
## Response: RESULT
## Sum Sq Df F value Pr(>F)
## (Intercept) 5851.4 1 2399.7704 < 2.2e-16 ***
## MATRIX 149.7 1 61.4003 1.248e-13 ***
## LOCATION 339.5 4 34.8078 < 2.2e-16 ***
## MATRIX:LOCATION 93.0 4 9.5304 3.377e-07 ***
## Residuals 624.2 256
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Now, let’s perform two-way ANOVA on the log-transformed data.
# ANOVA procedure on log-transformed data
aov.log <- aov(
log(RESULT) ~ MATRIX * LOCATION, data = dat,
contrasts = list(
MATRIX = 'contr.sum',
LOCATION = 'contr.sum'
)
)
Anova(aov.log, type = 'III')
## Anova Table (Type III tests)
##
## Response: log(RESULT)
## Sum Sq Df F value Pr(>F)
## (Intercept) 479.08 1 4379.867 < 2.2e-16 ***
## MATRIX 8.24 1 75.355 4.684e-16 ***
## LOCATION 14.40 4 32.914 < 2.2e-16 ***
## MATRIX:LOCATION 4.63 4 10.571 6.079e-08 ***
## Residuals 28.00 256
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Finaly, let’s perform two-way ANOVA on the rank-transformed data. Ranking is one of many procedures used to transform data that do not meet the assumptions of normality. Conover and Iman (1981) provided a review of the four main types of rank transformations. One method replaces each original data value by its rank (from 1 for the smallest to N for the largest, where N is the combined data sample size). This rank-based procedure has been recommended as being robust to non-normal errors, resistant to outliers, and highly efficient for many distributions.
# ANOVA procedure on rank-transformed data
aov.rnk <- aov(
rank(RESULT) ~ MATRIX * LOCATION, data = dat,
contrasts = list(
MATRIX = 'contr.sum',
LOCATION = 'contr.sum'
)
)
Anova(aov.rnk, type = 'III')
## Anova Table (Type III tests)
##
## Response: rank(RESULT)
## Sum Sq Df F value Pr(>F)
## (Intercept) 2911804 1 936.506 < 2.2e-16 ***
## MATRIX 168683 1 54.252 2.419e-12 ***
## LOCATION 442327 4 35.566 < 2.2e-16 ***
## MATRIX:LOCATION 101199 4 8.137 3.431e-06 ***
## Residuals 795960 256
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
The results indicate that soil depth (MATRIX), site location (LOCATION), and the interaction between depth and location (MATRIX:LOCATION) are statistically significant (p-value < 0.05). Let’s inspect the grand means and the group means.
model.tables(aov.org, type = "means", se = TRUE)
## Tables of means
## Grand mean
##
## 5.840902
##
## MATRIX
## SS SB
## 6.463 5.289
## rep 125.000 141.000
##
## LOCATION
## RA1 RA2 RA3 RA4 RA5
## 5.567 7.069 3.312 6.265 6.659
## rep 48.000 36.000 50.000 32.000 100.000
##
## MATRIX:LOCATION
## LOCATION
## MATRIX RA1 RA2 RA3 RA4 RA5
## SS 6.37 8.54 3.59 7.21 6.60
## rep 25.00 25.00 25.00 25.00 25.00
## SB 4.82 4.58 3.10 4.57 6.33
## rep 23.00 11.00 25.00 7.00 75.00
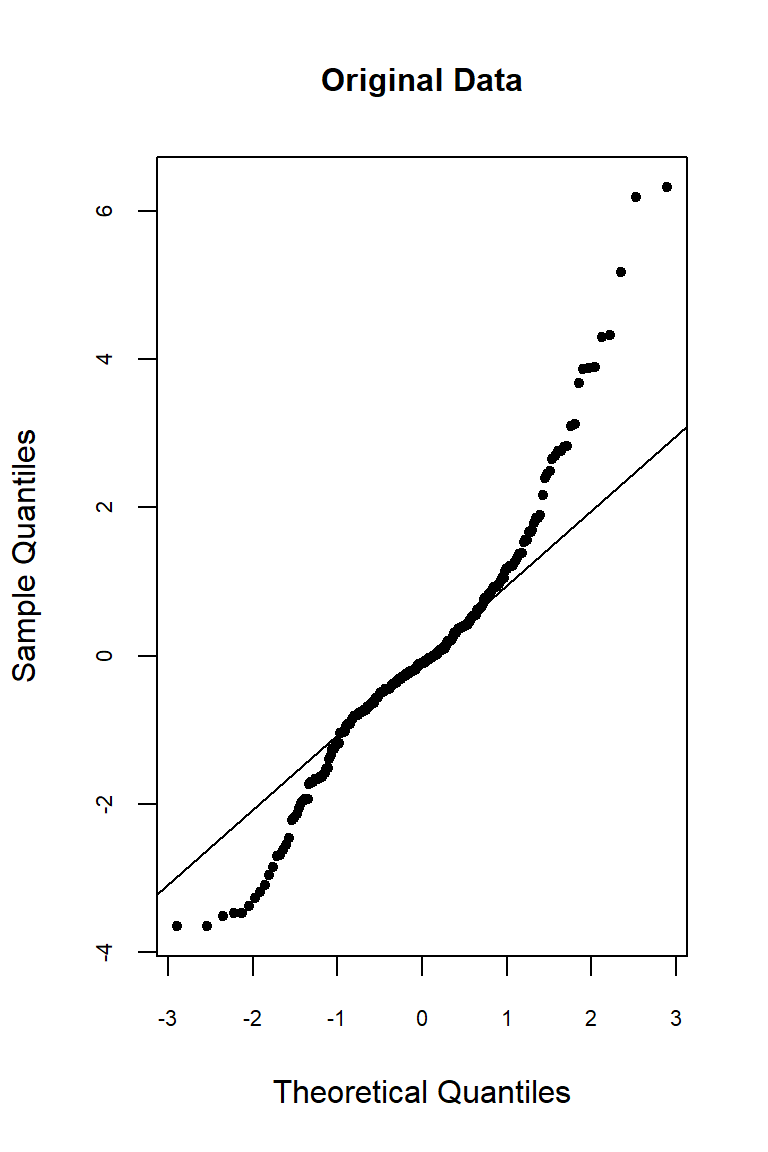
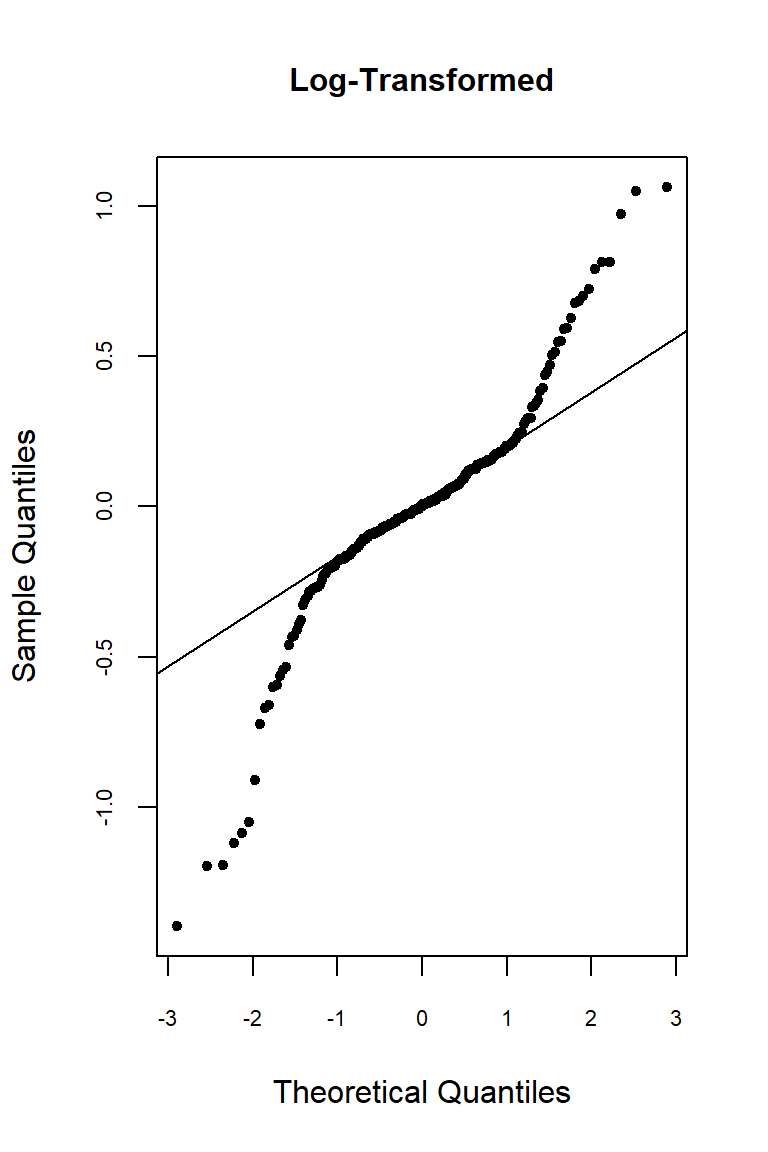
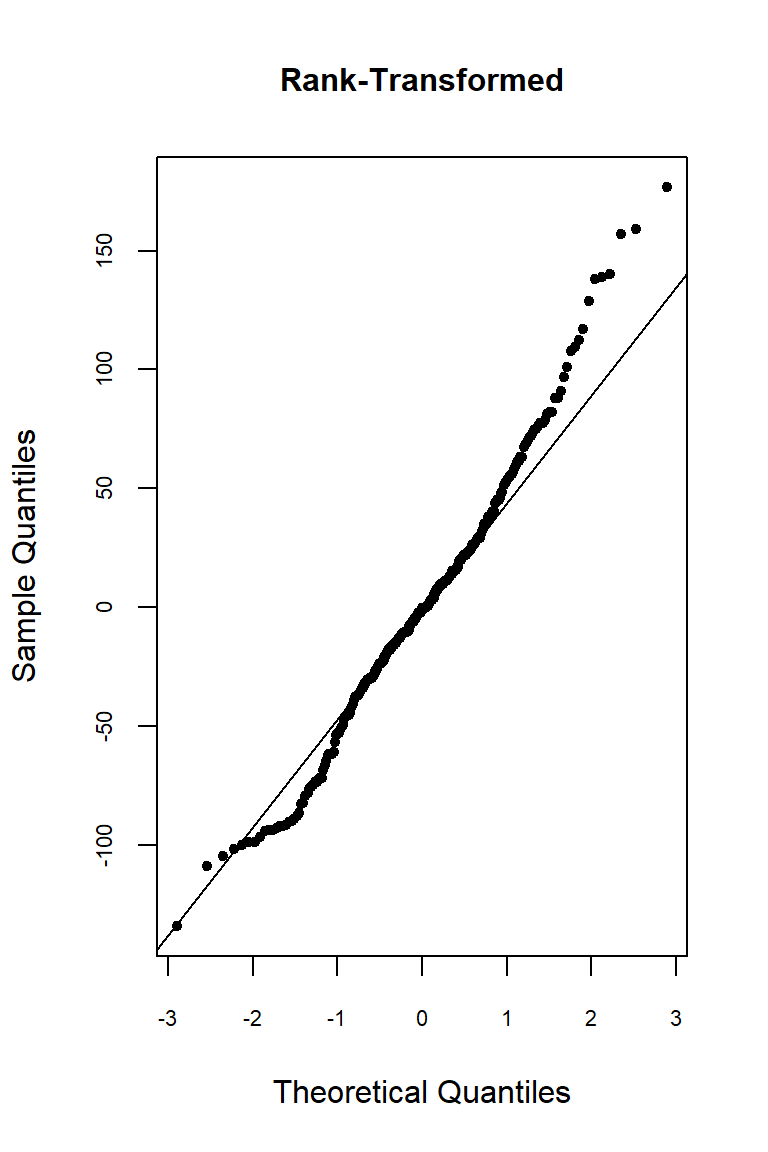
Let’s inspect the residuals from each model for normality. The residuals from the models using the orginal data and the log-transformed data deviate signficantly form nonmality. Residuals from the rank-transformed data model appear much better, although ranks aren’t expected to be normally distributed; barring any ties, ranks within any given group act like a sample without replacement from a discrete uniform distribution.
res.org = aov.org$resid
res.log = aov.log$resid
res.rnk = aov.rnk$resid
qqnorm(
res.org, pch = 20, main = "Original Data",
cex.lab = 1, cex.axis = 0.7, cex.main = 1
)
qqline(res.org)
qqnorm(
res.log, pch = 20, main = "Log-Transformed",
cex.lab = 1, cex.axis = 0.7, cex.main = 1
)
qqline(res.log)
qqnorm(
res.rnk, pch = 20, main = "Rank-Transformed",
cex.lab = 1, cex.axis = 0.7, cex.main = 1
)
qqline(res.rnk)
Now, let’s inspect the residuals versus the fitted values as a visual check for homogeneity of variances.
plot(aov.org, 1, main = "Original Data")
plot(aov.log, 1, main = "Log-Transformed")
plot(aov.rnk, 1, main = "Rank-Transformed")
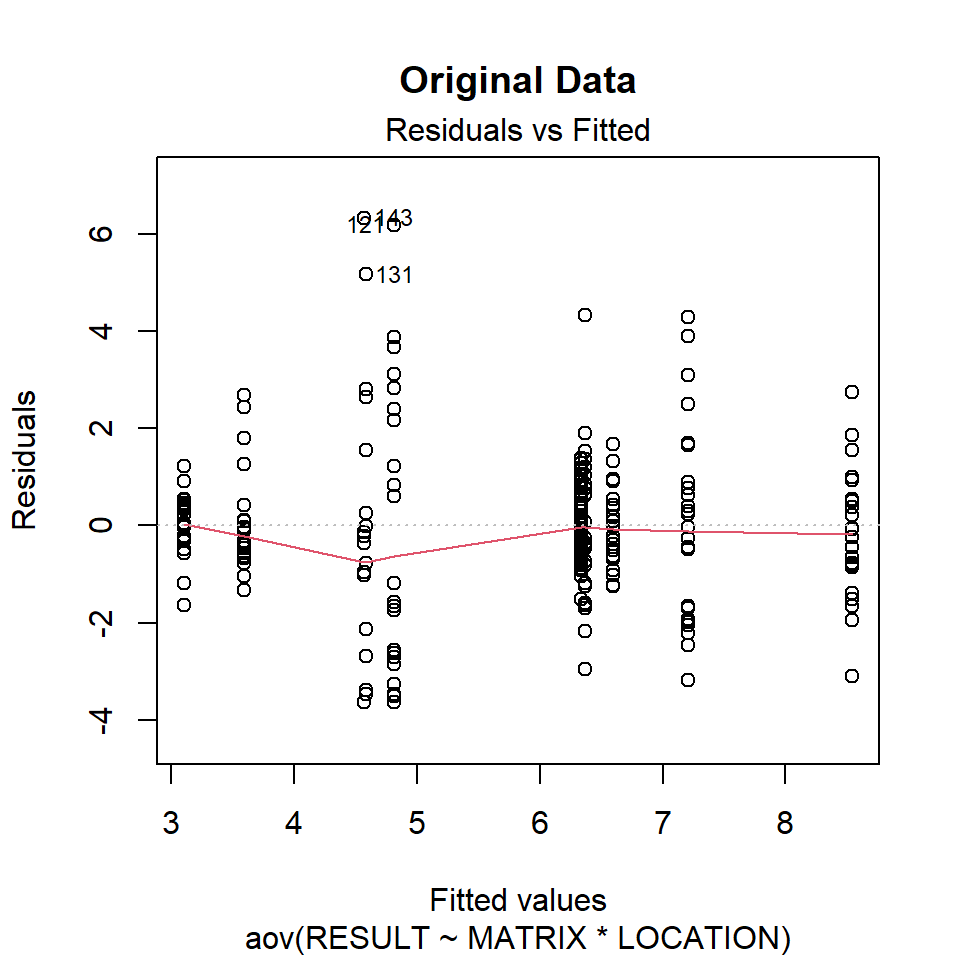
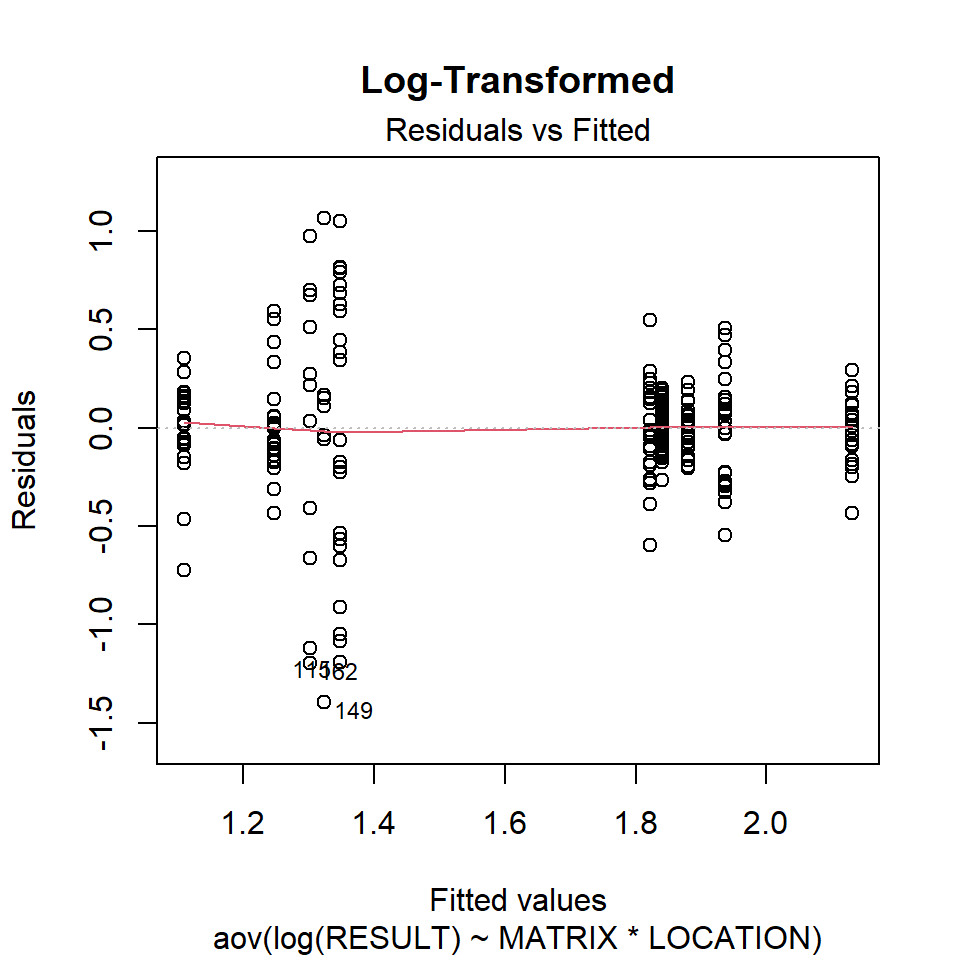
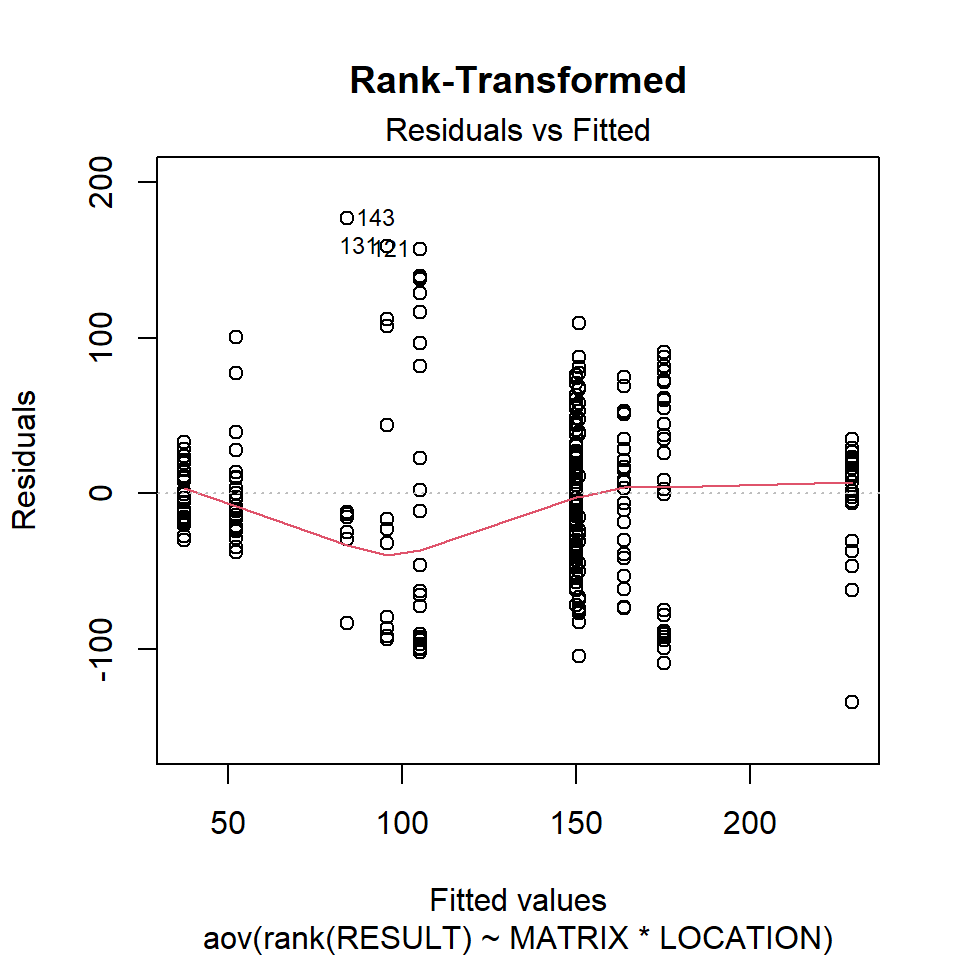
There is no evident relationships between residuals and the fitted values. Several points are identified as outliers, which can affect normality and homogeneity of variance.
Nature of Interactions
Let’s inspect the nature of the interactions using the R package emmeans. The emmeans package includes functions to facilitate post-hoc comparisons and contrast analysis. Let’s compare LOCATION separately for each MATRIX. The first thing to investigate is the significance of the interaction. If it is nonsignificant, we can focus on the main effects. However, if the interaction is significant, the main effects will not be helpful, as we will need to explore when each factor is significant given the levels of the other factor.
# Compute estimated marginal means for factor combinations
library(emmeans)
emmeans(aov.rnk, pairwise ~ LOCATION | MATRIX)
## $emmeans
## MATRIX = SS:
## LOCATION emmean SE df lower.CL upper.CL
## RA1 150.7 11.15 256 128.8 172.7
## RA2 229.3 11.15 256 207.4 251.3
## RA3 52.2 11.15 256 30.2 74.1
## RA4 175.1 11.15 256 153.2 197.1
## RA5 163.7 11.15 256 141.7 185.7
##
## MATRIX = SB:
## LOCATION emmean SE df lower.CL upper.CL
## RA1 105.0 11.63 256 82.1 127.9
## RA2 95.7 16.81 256 62.6 128.8
## RA3 37.2 11.15 256 15.2 59.1
## RA4 84.0 21.08 256 42.5 125.5
## RA5 150.0 6.44 256 137.3 162.7
##
## Results are given on the rank (not the response) scale.
## Confidence level used: 0.95
##
## $contrasts
## MATRIX = SS:
## contrast estimate SE df t.ratio p.value
## RA1 - RA2 -78.62 15.8 256 -4.985 <.0001
## RA1 - RA3 98.54 15.8 256 6.248 <.0001
## RA1 - RA4 -24.40 15.8 256 -1.547 0.5328
## RA1 - RA5 -12.98 15.8 256 -0.823 0.9234
## RA2 - RA3 177.16 15.8 256 11.233 <.0001
## RA2 - RA4 54.22 15.8 256 3.438 0.0061
## RA2 - RA5 65.64 15.8 256 4.162 0.0004
## RA3 - RA4 -122.94 15.8 256 -7.795 <.0001
## RA3 - RA5 -111.52 15.8 256 -7.071 <.0001
## RA4 - RA5 11.42 15.8 256 0.724 0.9508
##
## MATRIX = SB:
## contrast estimate SE df t.ratio p.value
## RA1 - RA2 9.29 20.4 256 0.455 0.9911
## RA1 - RA3 67.86 16.1 256 4.212 0.0003
## RA1 - RA4 21.02 24.1 256 0.873 0.9065
## RA1 - RA5 -44.96 13.3 256 -3.383 0.0073
## RA2 - RA3 58.57 20.2 256 2.903 0.0325
## RA2 - RA4 11.73 27.0 256 0.435 0.9925
## RA2 - RA5 -54.26 18.0 256 -3.014 0.0235
## RA3 - RA4 -46.84 23.8 256 -1.964 0.2865
## RA3 - RA5 -112.83 12.9 256 -8.762 <.0001
## RA4 - RA5 -65.99 22.0 256 -2.994 0.0249
##
## Note: contrasts are still on the rank scale
## P value adjustment: tukey method for comparing a family of 5 estimates
We see that the effect of MATRIX depends on the levels of LOCATION and vice versa. The next step is to determine the nature of the interaction. Let’s perform something akin to a one-way ANOVA for MATRIX within each level of LOCATION. However, the F-test will utilize all of the information from the full two-way factorial model.
em_out_category <- emmeans(aov.rnk, ~ MATRIX | LOCATION)
print(em_out_category)
## LOCATION = RA1:
## MATRIX emmean SE df lower.CL upper.CL
## SS 150.7 11.15 256 128.8 172.7
## SB 105.0 11.63 256 82.1 127.9
##
## LOCATION = RA2:
## MATRIX emmean SE df lower.CL upper.CL
## SS 229.3 11.15 256 207.4 251.3
## SB 95.7 16.81 256 62.6 128.8
##
## LOCATION = RA3:
## MATRIX emmean SE df lower.CL upper.CL
## SS 52.2 11.15 256 30.2 74.1
## SB 37.2 11.15 256 15.2 59.1
##
## LOCATION = RA4:
## MATRIX emmean SE df lower.CL upper.CL
## SS 175.1 11.15 256 153.2 197.1
## SB 84.0 21.08 256 42.5 125.5
##
## LOCATION = RA5:
## MATRIX emmean SE df lower.CL upper.CL
## SS 163.7 11.15 256 141.7 185.7
## SB 150.0 6.44 256 137.3 162.7
##
## Results are given on the rank (not the response) scale.
## Confidence level used: 0.95
Next, we pipe this object into the pairs() function and use the joint = TRUE option in the test() function to get the joint test of significance (i.e., the ANOVA F-test). The test function is similar to running multiple one-way ANOVAs, except we are using the error term from the full two-way factorial model. The results include the following:
- df1: degrees of freedom between groups
- df2: degrees of freedom within groups
- F.ratio: F statistic for MATRIX within each level of LOCATION
- p.value: probability of a Type-I error for each category
em_out_category %>%
pairs() %>%
test(joint = TRUE)
## LOCATION df1 df2 F.ratio p.value
## RA1 1 256 8.046 0.0049
## RA2 1 256 43.861 <.0001
## RA3 1 256 0.907 0.3418
## RA4 1 256 14.604 0.0002
## RA5 1 256 1.134 0.2879
We find that MATRIX is significant for RA1, RA2, and RA4; the effect of MATRIX is not significant for RA3 and RA5. Because MATRIX only has two levels, we do not need to do any further pairwise comparisons. The following code tells us which pairwise difference led to the significant joint F-test.
pairs(em_out_category)
## LOCATION = RA1:
## contrast estimate SE df t.ratio p.value
## SS - SB 45.7 16.1 256 2.837 0.0049
##
## LOCATION = RA2:
## contrast estimate SE df t.ratio p.value
## SS - SB 133.6 20.2 256 6.623 <.0001
##
## LOCATION = RA3:
## contrast estimate SE df t.ratio p.value
## SS - SB 15.0 15.8 256 0.952 0.3418
##
## LOCATION = RA4:
## contrast estimate SE df t.ratio p.value
## SS - SB 91.1 23.8 256 3.821 0.0002
##
## LOCATION = RA5:
## contrast estimate SE df t.ratio p.value
## SS - SB 13.7 12.9 256 1.065 0.2879
##
## Note: contrasts are still on the rank scale
Multiple Comparisons
Although the original two-way ANOVA indicated evidence of interaction between soil depth (MATRIX) and site (LOCATION), let’s perform multiple comparisons using the glht() function in the R package multcomp. glht stands for general linear hypothesis tests and is used to perform multiple pairwise-comparisons for parametric models. Let’s perform post-hoc pairwise-comparisons between the means of groups using the Tukey Honest Significant Differences (HSD) test. We don’t need to perform the test for MATRIX because it has only two levels, which have been shown to be significantly different by the ANOVA test. Therefore, the Tukey HSD test will be done only for LOCATION.
library(multcomp)
summary(glht(aov.rnk, linfct = mcp(LOCATION = "Tukey")))
##
## Simultaneous Tests for General Linear Hypotheses
##
## Multiple Comparisons of Means: Tukey Contrasts
##
##
## Fit: aov(formula = rank(RESULT) ~ MATRIX * LOCATION, data = dat, contrasts = list(MATRIX = "contr.sum",
## LOCATION = "contr.sum"))
##
## Linear Hypotheses:
## Estimate Std. Error t value Pr(>|t|)
## RA2 - RA1 == 0 34.663 12.909 2.685 0.0572 .
## RA3 - RA1 == 0 -83.201 11.273 -7.381 <0.001 ***
## RA4 - RA1 == 0 1.689 14.388 0.117 1.0000
## RA5 - RA1 == 0 28.972 10.312 2.809 0.0410 *
## RA3 - RA2 == 0 -117.864 12.804 -9.205 <0.001 ***
## RA4 - RA2 == 0 -32.974 15.617 -2.111 0.2136
## RA5 - RA2 == 0 -5.690 11.967 -0.475 0.9892
## RA4 - RA3 == 0 84.890 14.294 5.939 <0.001 ***
## RA5 - RA3 == 0 112.173 10.180 11.019 <0.001 ***
## RA5 - RA4 == 0 27.283 13.550 2.014 0.2569
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- single-step method)
The results indicate that arsenic concentrations in soil at location RA3 are statistically different than those at the other four site locations.
References
Conover, W.J. and R.L. Iman, R. L. 1981. Rank transformations as a bridge between parametric and nonparametric statistics. American Statistician. 35 (3): 124-129.
- Posted on:
- April 16, 2022
- Length:
- 17 minute read, 3441 words
- See Also: