Test for Stochastic Dominance Using the Wilcoxon Rank Sum Test
By Charles Holbert
March 7, 2025
Introduction
In the realm of statistical analysis, the two-sample Wilcoxon Rank Sum (WRS) test (also known as Mann-Whitney test) is commonly referred to as the nonparametric counterpart to the two-sample t-test, often associated with testing the equality of medians. However, this interpretation is somewhat misleading, as the test fundamentally evaluates whether one distribution stochastically dominates another. In simpler terms, it assesses whether values drawn from one group are consistently greater than those from another, reflecting a dominance in their distribution. To clarify this concept, we’ll conduct a simulation using two samples with identical medians yet differing distributions, all within the R environment for statistical computing and visualization. This exploration aims to reveal the true nature of the WRS test beyond its frequent mischaracterization.
Background
The WRS test is often viewed as a nonparametric alternative to the two-sample t-test. Whereas the null hypothesis of the two-sample t-test is equal means, the null hypothesis of the Wilcoxon test is usually assumed as equal medians. However, this is only true in the rarest of cases in which the population distributions of the two groups are merely shifted versions of each other (i.e., differing only in location, and not shape or scale).
The t-test explicitly makes use of the presumed parametric (normal) distribution for the two groups being compared. Thus, the t-test is a test of means, both conceptually and computationally. The WRS test is a nonparametric method that typically does not rely on a specific distribution, but the procedure is based on certain assumptions concerning those distributions. One critical assumption is that the variances of the two distributions must be equal (Pratt 1964).
In general, the null hypothesis for the WRS test is expressed as: Ho: Distribution F = Distribution G. The alternative hypothesis is formulated as: Ha: G(x) = F(x + delta), where delta is not equal to 0. This represents a distinct “shift alternative,” assuming that the shape and scale of both distributions are identical. In this context, delta signifies the difference between the population medians. Although this provides a valid and somewhat limited basis for interpreting the WRS procedure as a test of medians, its importance is somewhat lessened when we acknowledge that, under the shift hypothesis, delta also reflects the difference in means, percentiles, or any other measure of central tendency or location between the two distributions (Divine et al. 2018).
Rather than concentrating on summary statistics specific to samples, the WRS test evaluates the entire distributions. Consequently, it is sensitive to various characteristics of the data, including the shape of the distribution. While the test is commonly linked to median comparison, it is more precise to state that it determines whether one distribution stochastically dominates the other. Stochastic dominance indicates that if one distribution dominates another, values sampled from the first distribution are more likely to be larger than those from the second. Thus, a more accurate description of the WRS test is given by Forthofer, Lee, and Hernandez (2007), who state: This test is used to determine whether or not the probability that a randomly selected observation from one population is greater than a randomly selected observation from another population is equal to 0.5.
Data
To illustrate that the WRS procedure is a test of stochastic dominance, a simulation is conducted featuring two samples that have the same medians yet exhibit significantly different distributions. In one group, the data follow an exponential distribution with a mean of 1, resulting in a median of log 2. In the other group, the data are normally distributed with both a mean and median of log 2 and a variance of 1. For this simulation, 100 observations are generated for each sample and compared using the WRS test.
# Load libraries
library(dplyr)
library(ggplot2)
library(scales)
library(ggstatsplot)
# Simulate two separate vectors of data
set.seed(2376)
x <- rexp(100)
y <- rnorm(100) + log(2)
# Put observations into a single vector and make a group indicator vector
dat <- data.frame(
Result = c(x, y),
Group = as.factor(c(rep('x', 100), rep('y', 100)))
)
Descriptive statistics for the two data sets are provided below. Descriptive statistics include the total number of observations; the minimum and maximum values; and the mean, median, standard deviation, and coefficient of variation (CV). The mean and median provide a measure of central tendency, while the standard deviation and CV provide a measure of variability in the data. The CV is the ratio of the sample standard deviation to the sample mean and thus indicates whether the amount of “spread” in the data is small or large relative to the average observed magnitude.
# Compute summary statistics
cdat <- dat %>%
group_by(Group) %>%
summarise(
count = n(),
min = round(min(Result, na.rm = TRUE), 2),
max = round(max(Result, na.rm = TRUE), 2),
mean = round(mean(Result, na.rm = TRUE), 2),
median = round(median(Result, na.rm = TRUE), 2),
sd = round(sd(Result, na.rm = TRUE), 2),
cv = round(sd/mean, 2),
) %>%
ungroup() %>%
data.frame()
# Create table
library(kableExtra)
kbl(cdat) %>%
kable_minimal(full_width = F, position = "left", html_font = "Cambria")
| Group | count | min | max | mean | median | sd | cv |
|---|---|---|---|---|---|---|---|
| x | 100 | 0.00 | 5.99 | 1.1 | 0.77 | 1.12 | 1.02 |
| y | 100 | -1.95 | 2.86 | 0.6 | 0.77 | 1.05 | 1.75 |
Graphical Comparisons
A combination of box and violin plots for each data set are provided below. Box plots show the central tendency, degree of symmetry, range of variation, and potential outliers of a data set. The box itself spans from the first quartile to the third quartile, and the line inside the box represents the median. Lines extending from the box, called whiskers, show the range of the data. If extensive overlap exists between the box plots from different data groups then the measurements from each group, on average, are similar. Conversely, little overlap between data groups, suggests that group measurements are, on average, different. While box plots show the difference in concentrations, paired information is lost. Violin plots combine the features of a box plot with a kernel density plot. It not only shows summary statistics (e.g., median, quartiles, and range) but also provides an estimate of the probability density of the data at different values.
# Create combination box and violin plot
ggbetweenstats(
data = dat,
x = Group, y = Result,
type = 'nonparametric',
pairwise.comparisons = TRUE,
conf.level = 0.95,
p.adjust.method = 'none',
pairwise.display = 's',
centrality.point.args = list(size = 3, color = 'darkred'),
xlab = 'Group',
ylab = 'Result',
title = 'Comparison of Group Results',
subtitle = 'Test Data',
results.subtitle = FALSE
) +
theme_bw() +
theme(
plot.title = element_text(size = 14, margin = margin(b = 2)),
plot.subtitle = element_text(size = 12, margin = margin(b = 3), face = 'italic'),
axis.title = element_text(size = 12, color = 'black'),
axis.text = element_text(size = 10, color = 'black')
)
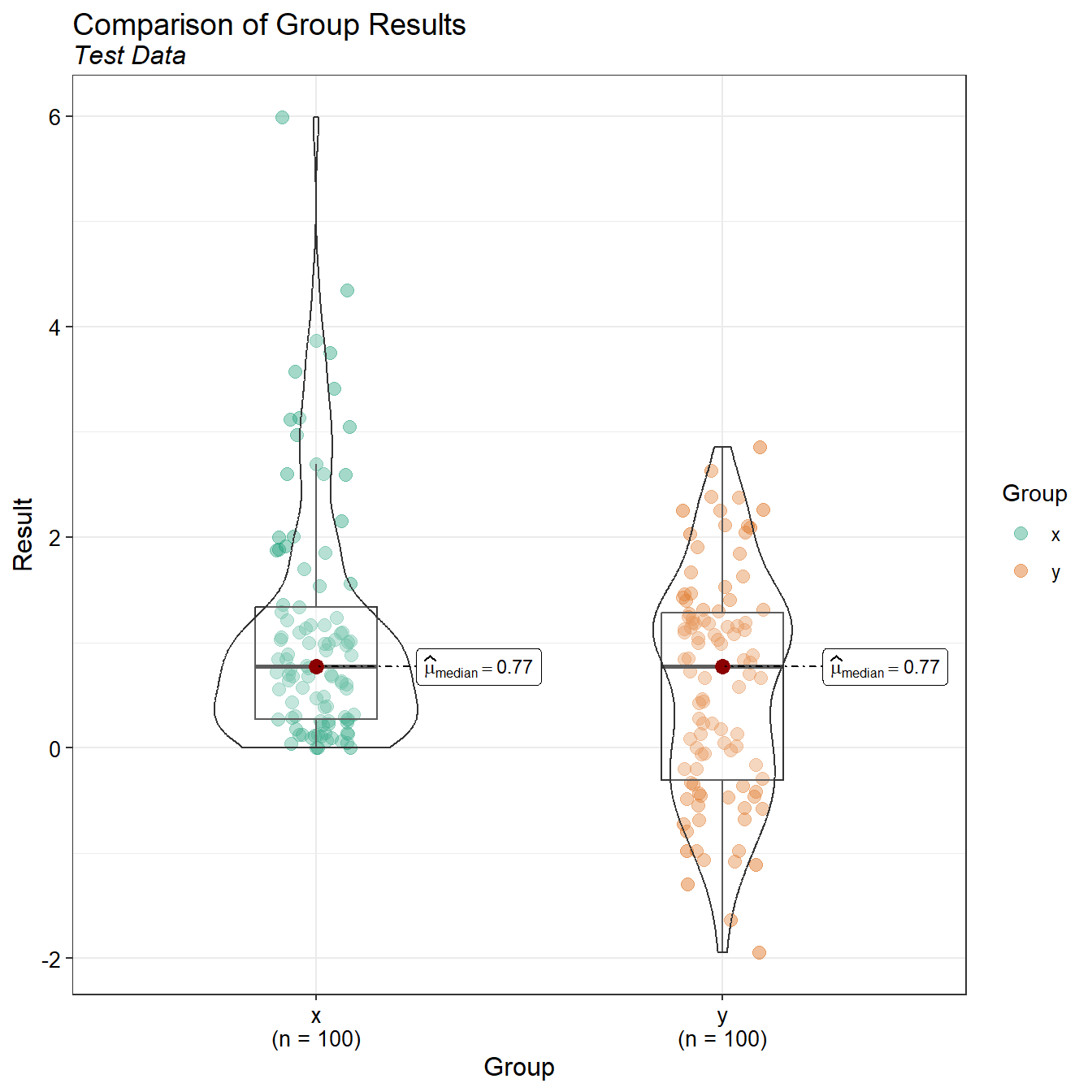
A comparison of the two data sets according to their empirical cumulative distribution function (ECDF) is provided below. Plots of the ECDF show the cumulative distribution of one or more data sets without assuming a specific distribution form. An ECDF displays data points from lowest to highest against their percentiles and is effective for comparing different data distributions. Overlapping ECDF plots allow for direct comparison by plotting multiple ECDFs on the same graph, enabling observation of intersections and divergences in the data distributions.
# Plot empirical cumulative distribution functions (ecdfs)
ggplot(data = dat, aes(x = Result, color = Group)) +
stat_ecdf(lwd = 1, geom = 'line') +
scale_x_continuous(labels = function(x) format(x, big.mark = ",",
scientific = FALSE)) +
labs(title = 'ECDF Plot',
subtitle = 'Test Data',
color = NULL,
x = 'Result',
y = 'Cumulative Probability') +
theme_bw() +
theme(aspect.ratio = 1) +
scale_color_manual(values = c('#1B9A89', '#C37E08')) +
theme(plot.title = element_text(margin = margin(b = 2), size = 14, hjust = 0,
color = 'black', face = 'bold'),
plot.subtitle = element_text(margin = margin(b = 3), size = 12, hjust = 0,
color = 'black', face = 'italic'),
axis.title = element_text(size = 12, color = 'black'),
axis.text = element_text(size = 11, color = 'black'),
legend.justification = c(1, 0),
legend.position = 'inside', legend.position.inside = c(0.98, 0.03),
legend.text = element_text(size = 12),
legend.key.height = unit(1.2, 'line'))
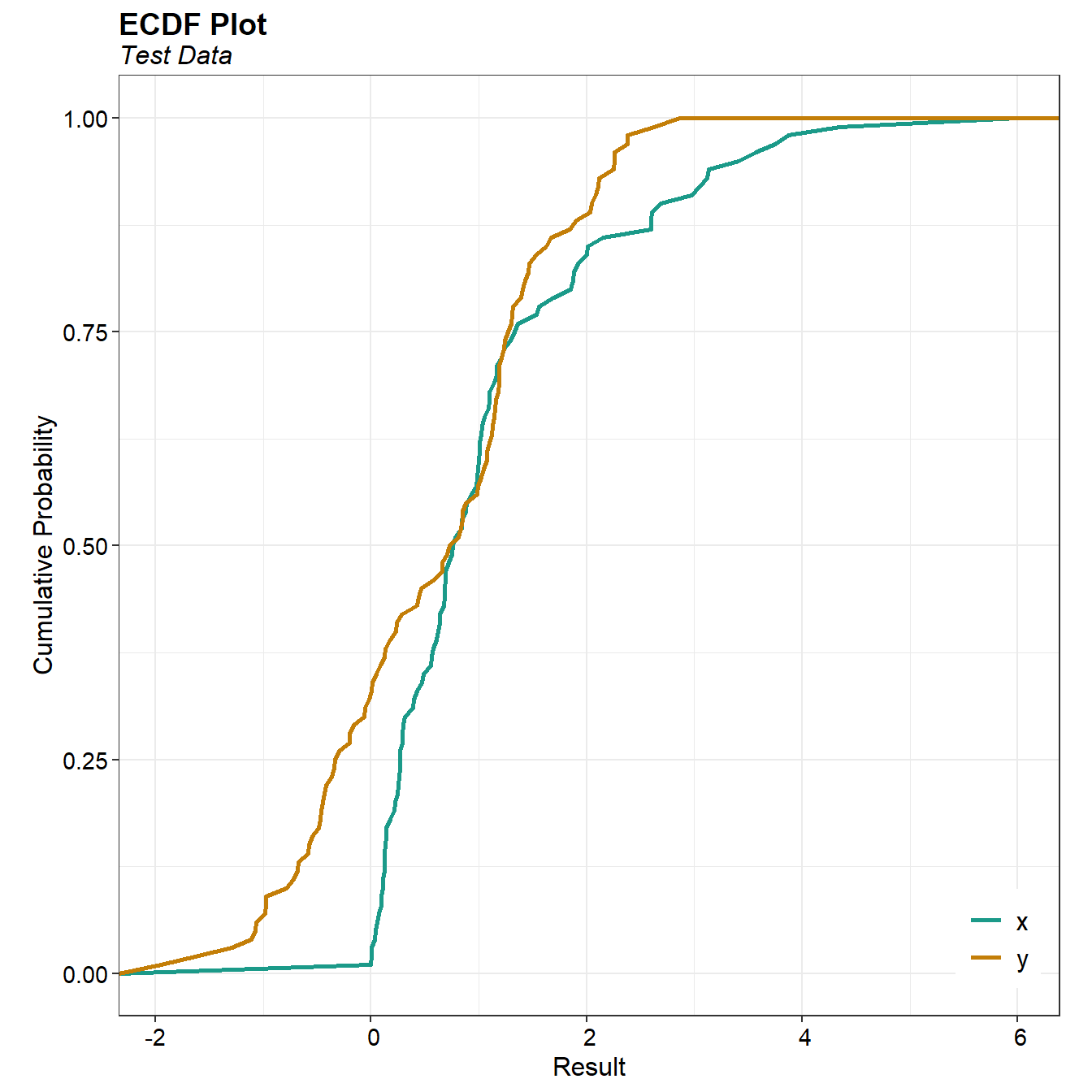
The y-data cumulative distribution (green line) lies on or to the right of the x-data cumulative distribution (orange line) at most all points. This indicates the y-data distribution stochastically dominates the x-data distribution, meaning the y-data distribution is likely to be larger than the x-data distribution at any given point.
WRS Test
Results from the two-sample WRS test are provided below. The test combines the observations from both samples and ranks them from smallest to largest. The procedure transforms the data into their relative positions within the combined data set. The test then calculates the sum of the ranks for one of the samples. This sum reflects the overall tendency of that sample’s values to be higher or lower than the other sample’s values. If the rank sum for one sample is significantly higher, it suggests that the values in that sample tend to be larger than the values in the other sample. Conversely, a significantly lower rank sum suggests the opposite.
# Perform wilcox test
wilcox.test(
x, y,
alternative = 'two.sided',
conf.int = TRUE,
conf.level = 0.95
)
##
## Wilcoxon rank sum test with continuity correction
##
## data: x and y
## W = 5910, p-value = 0.02627
## alternative hypothesis: true location shift is not equal to 0
## 95 percent confidence interval:
## 0.03637324 0.69339791
## sample estimates:
## difference in location
## 0.3822294
The WRS test indicates a small p-value, suggesting that it’s not the medians that differ, but rather that one of the two distributions tends to have higher values overall.
Quantile Regression
If our interest actually is focused on the medians, an appropriate test that is not sensitive to the shape of the distribution is quantile regression. Quantile regression examines the relationship between specific conditional quantiles (like the median) of a response variable and independent variable, as opposed to just estimating the mean. This technique is more robust to outliers in the response variable and provides insights across the entire distribution, rather than focusing solely on average values. Quantile regression on the simulated data is performed below.
# Load quantreg package and use rq() function to fit the median regression
library(quantreg)
summary(rq(Result ~ Group, data = dat))
##
## Call: rq(formula = Result ~ Group, data = dat)
##
## tau: [1] 0.5
##
## Coefficients:
## coefficients lower bd upper bd
## (Intercept) 0.75905 0.66751 0.98662
## Groupy 0.05527 -0.44725 0.28746
The results from quantile regression indicate that we cannot reject the null hypothesis of equal medians.
Bootstrapping
Bootstrapping is an effective nonparametric approach for deriving confidence intervals for various statistics such as the mean, median, or standard deviation, independent of the underlying data distribution (Efron and Tibshirani 1993). The process of bootstrapping the medians of two independent samples is relatively straightforward. First, bootstrap each sample separately to create the sampling distribution for each median. Then, calculate the differences between these medians to establish the sampling distribution of the differences, which is the primary focus. Using this distribution, a confidence interval can be calculated. If the resulting confidence interval does not include zero, the null hypothesis, which asserts that there is no difference between the medians of the two groups, can be rejected.
First we create a function to calculate the difference in medians. The function will resample the data according to randomly selected row numbers and return the difference in medians for the resampled data. We’ll use the function to resample the data 1,000 times, taking a difference in medians each time, and saving the results.
# Bootstrap function
library(boot)
med.diff <- function(d, i) {
tmp <- d[i,]
median(tmp$Result[tmp$Group == 'y']) -
median(tmp$Result[tmp$Group == 'x'])
}
# Perform bootstrapping
set.seed(2376)
boot.out <- boot(data = dat, statistic = med.diff, R = 1000)
Taking the median of those 1,000 differences in medians gives a point estimate of the estimated difference in medians.
median(boot.out$t)
## [1] -0.03137753
Confidence intervals for the differences in medians are shown below. Four different confidence intervals are generated based on the bootstrap results. These intervals consist of: (1) the first-order normal approximation, which assumes that the distribution of the bootstrapped medians follows a normal distribution; (2) the basic bootstrap interval, which assumes that there is no bias between the median of the original data sample and the mean of the bootstrapped medians (i.e., they are equal); (3) the bootstrap percentile interval, which assumes that the distribution of the medians is symmetrical; and (4) the adjusted bootstrap percentile (BCa) interval, which accounts for bias and imposes fewer assumptions about the bootstrap distribution.
boot.ci(boot.out)
## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 1000 bootstrap replicates
##
## CALL :
## boot.ci(boot.out = boot.out)
##
## Intervals :
## Level Normal Basic
## 95% (-0.3983, 0.5043 ) (-0.3430, 0.5989 )
##
## Level Percentile BCa
## 95% (-0.5991, 0.3428 ) (-0.5048, 0.3832 )
## Calculations and Intervals on Original Scale
The confidence intervals using the four different computational methods are relatively the same. The intervals all include zero, indicating that the null hypothesis of no difference between the medians of the two sample group can not be rejected.
Conclusions
The WRS test is often perceived as a median comparison procedure based on the assumption that two populations differ only by a consistent shift, a condition that is infrequently met in practice. This perception is reinforced by conventions linking normally distributed data with means and t-tests, while skewed data is aligned with medians and WRS tests. The test’s focus on rankings further contributes to the median comparison interpretation, despite different ranking methodologies being used.
Assuming that distributions differ solely by location shift simplifies the mathematics of the test, but is generally unrealistic for many applications. The WRS test essentially evaluates if one set of observations tends to be greater than another, implying one population “dominates” the other regarding distribution. If data do not meet the test’s requirements of symmetry or similar distributions, the accuracy of median comparisons may be compromised, potentially increasing the Type I error rate. For situations involving non-symmetric data, alternatives like quantile regression or bootstrapping offer a flexible, nonparametric option for testing hypotheses about various statistics without relying on rank transformations.
References
Divine, G.W., H.J. Norton, A.E. Baron, and E.J. Colunga. 2018. The Wilcoxon-Mann-Whitney Procedure Fails as a Test of Medians. The Americian Statistician, 72, 278-286.
Efron, B. and R.J. Tibshirani. 1993. An Introduction to the Bootstrap. Chapman & Hall, New York.
Forthofer, R., E. Lee, and M. Hernandez. 2007. Biostatistics: A Guide to Design, Analysis, and Discovery (2nd ed.). Elsevier Academic Press, Amsterdam.
Pratt, J. 1964). Robustness of Some Procedures for the Two-Sample Location Problem. JASA, 59, 665- 680.
- Posted on:
- March 7, 2025
- Length:
- 12 minute read, 2441 words
- See Also: